TABVLA RASA

JENENSER ZEITSCHRIFT FÜR KRITISCHES DENKEN

Ausgabe 44

August 2011

Artikel als PDF

[Nächster Artikel]

Hauptmenü

Archiv

Allgemein, nicht formal

Über einen grundlegenden Unterschied zwischen Freges Begriffsschrift und der modelltheoretischen Logik

Tabea Rohr

1  Quantifikation ohne Quantor

Gottlob Frege gilt gemein hin als der Begründer der Quantorenlogik. Richtig daran ist, dass man in seiner Begriffsschrift aus dem Jahre 1879 erstmals ein Axiomensystem für die vollständige Axiomatisierung der Prädikatenlogik erster Stufe findet. Nicht richtig ist hingegen, dass das Höhlungszeichen nur eine andere Schreibweise für das ist, was man heute als Quantor bezeichnet. Dieser Gedanke ist nicht neu. Polimenov gab in seinem Aufsatz „Gibt es wirklich Quantoren in Freges Quantifikationstheorie?“¹ schon eine negative Antwort auf seine Titelfrage. In seiner Begründung verweist Polimenov auf das Zeicheninventar von Freges Logik. Anders als in der mathematischen Logik der Gegenwart gebe es in der Begriffsschrift keinen Unterschied von gebundenen und freien Variablen. Die Buchstaben, die in Freges Logik fälschlicherweise mit den freien Variablen identifiziert werden, seien keine bloßen Platzhalter, die erst an einen Individuenbereich „gebunden“ werden, sondern drücken bereits Allgemeinheit aus. Das Höhlungszeichen sei aus diesem Grund gar nicht in jedem Falle nötig, um eine Allaussage zu formalisieren. Deshalb, so Polimenov, seien die kleinen lateinischen Buchstaben die „Allgemeinheitsbuchstaben.“²

Im folgenden soll gezeigt werden, dass diese Problematik symptomatisch ist für einen grundlegenden Unterschied zwischen Freges Verständnis von Logik und dem der Modelltheorie, der eine bloße Transkription beider Systeme ineinander unmöglich und eine Übersetzung derselben schwierig macht.

2  Ein kurzer Vergleich der Begriffsschrift mit der modelltheoretischen Logik

Die Aussage Polimenovs, es gebe bei Frege keine Entsprechung für die freien und gebundenen Variablen, erscheint evident, vergleicht man die Begriffsschrift mit der modelltheoretischen Logik im Ganzen. Dabei lassen sich folgende, aufeinander aufbauende Unterschiede festmachen:

a) In der modelltheoretischen Logik wird zur Interpretation der Zeichen ein Individuenbereich festgelegt, nicht aber in der Begriffsschrift. Frege schränkt den Bereich seiner deutschen Buchstaben, die häufig mit den gebundenen Variablen gleichgesetzt werden, nur ein, indem er fordert, dass der gesamte Ausdruck Bedeutung gewinne, wenn man einen solchen deutschen Buchstaben „durch einen Namen ersetzt, der einen Gegenstand bedeutet“.³ Alle anderen Einschränkungen müssen in der Formel selbst explizit gemacht werden. Insofern muss man die Einschätzung, die man gelegentlich über Frege liest, dieser habe einen fixierten Individuenbereich,⁴ gar nicht als eine Einschränkung der Frege‘schen Logik betrachten. Mit Freges „fixiertem Individuenbe­reich“, wenn man in diesem Fall denn überhaupt von einem „Individuenbereich“ reden sollte, kann man von allen Gegenständen sprechen und somit jede Aussage treffen, die, zumindest nach Freges Referenztheorie, wahrheitswertfähig ist. Deshalb sollte darin nicht weniger als in jedem beliebig großem Individuenbereich ausgedrückt werden können.

b) Begriffsschriftaussagen mit lateinischen Buchstaben drücken schon immer wahrheitswertfähige Sätze aus, modelltheoretische Aussagen mit Variablen sind jedoch zunächst nur Aussageformen. Einer freien Variable ist in der modelltheoretischen Logik noch kein Individuenbereich zugewiesen, dadurch kann eine Formel, die eine solche Variable enthält, noch gar keine Aussage ausdrücken, denn es ist ja vollkommen unklar, was für eine freie Variable eingesetzt werden kann. Für Freges kleine lateinische bzw., in Freges Terminologie gesprochen, „unbestimmt andeutende“ Buchstaben, die fälschlicherweise häufig mit diesen freien Variablen identifiziert werden, ist dies hingegen immer festgelegt – jeder Name, der einen Gegenstand bedeutet.

c) Die Quantoren machen aus Satzformen allgemeine Sätze. Das Höhlungszeichen schränkt die Allgemeinheit auf bestimmte Teile der Formel ein. Da bei Frege auch Formeln ohne Höhlung, die einen kleinen lateinischen Buchstaben enthalten, Sätze und nicht bloß Aussageformen sind, ist Polimenovs Aussage, Freges vermeintliche Quantoren seien nicht die Operatoren, die aus einer Aussagefunktion eine generelle Aussage erzeugen,⁵ trivialerweise wahr. Das Höhlungszeichen ist neben den kleinen lateinischen Buchstaben zum Ausdruck der Allgemeinheit nur nötig, um die Allgemeinheit auf einen bestimmten Teil der Formel einzuschränken, damit etwa der Unterschied zwischen „alle nicht“ und „nicht alle“ oder verschachtelte Allgemeinheitsbeziehungen ausgedrückt werden können.⁶

3  Übersetzungsversuche

Im vorherigen Abschnitt sollte deutlich geworden sein, dass das Höhlungszeichen kein Quantor, die lateinischen Buchstaben keine freien Variablen und die deutschen Buchstaben keine gebundenen Variablen sind. Bei sogenannten „Transkriptionen“⁷ der Frege’schen in die moderne Notationsweise wird jedoch dieser Eindruck vermittelt. Freges Begriffsschrift unterscheidet sich aber von dem, was man in modernen Logiklehrbüchern findet, nicht einfach durch das Notationssystem, sondern sie besitzt ganz andere Grundbausteine. Will man also eine Formel der modelltheoretischen Logik in der Begriffsschrift darstellen oder umgekehrt, so ist dazu keine reine Transkriptions- sondern eine Übersetzungsleistung notwendig.

Ein Begriffsschriftsatz, wie

darf man in der modelltheoretischen Logik nicht einfach mit der Formel:

f(x)

wiedergeben, denn diese drückt im Gegensatz zur Begriffsschriftformel keinen Satz aus, sondern nur eine Aussageform. Die Übersetzung muss also, da der kleine lateinische Buchstabe in der Begriffsschriftformel Allgemeinheit ausdrückt, mit einem Quantor wiedergegeben werden:

⋀x:f(x)

Bei dieser Übersetzung ergibt sich wiederum die Frage, über welchen Individuenbereich der Quantor quantifizieren muss. Um der Begriffsschriftformel zu entsprechen, müsste der Individuenbereich die Menge aller Namen sein, die einen Gegenstand bedeuten. Ganz abgesehen davon, dass diese Menge unter Umständen nicht definiert werden kann,⁸ wäre der Wahrheitswert abhängig davon, welche Gegenstände es gibt. Eine Frage, die in der mathematischen Logik eigentlich nichts zu suchen hat.

Möchte man umgekehrt eine modelltheoretische Formel in Begriffsschrift darstellen, so muss man die Einschränkung auf den jeweiligen Individuenbereich explizit innerhalb der Begriffsschriftformel ausdrücken. Eine modelltheoretische Formel:

⋀x∊R:[P(x) → Q(x)]

könnte man in der Begriffsschrift darstellen, indem man die Zugehörigkeit zum Individuenbereich auch als Begriff auffasst und das Fallen unter diesen Begriff als Bedingung in die Begriffsschriftformel bringt:

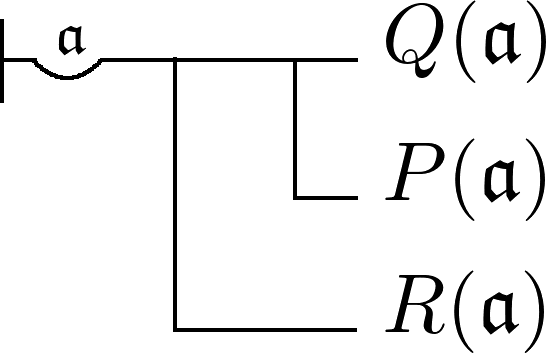
Diese Formel ist wiederum identisch ist mit:

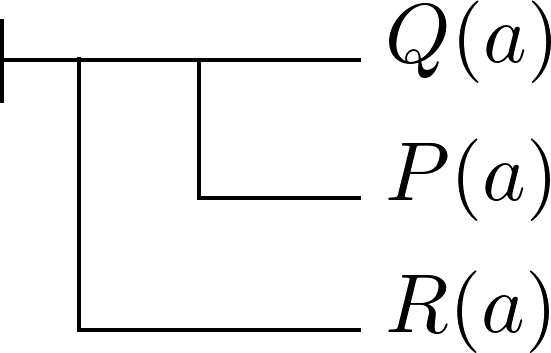
Diese Begriffsschriftformel ist zwar unter den gleichen Umständen wahr, wie die Ausgangsformel, sie ist jedoch trotzdem nicht einfach eine andere Schreibweise für jene. In der modelltheoretischen Formel wird ein klar umgrenzter Individuenbereich gegeben. Die Formel drückt aus, dass jeder Gegenstand dieses Individuenbereichs die Formel:

P(x) → Q(x)

erfüllen. Freges Begriffsschriftformel ist jedoch wahr, wenn alle Namen, die einen Gegenstand bedeuten, die Formel:

R(x) → [P(x) → Q(x)]

erfüllt. Damit wird etwas über alle Gegenstände überhaupt ausgedrückt und nicht über eine vorgegebene Menge.

Noch komplizierter wird es, möchte man eine Formel der modelltheoretischen Logik ohne angegebenen Individuenbereich wiedergeben, also etwa ein Axiom wie beispielsweise:

[⋀x: f(x)]→f(a)

Obwohl diese Regel nichteinmal eine freie Variable enthält, denn „a“ steht hier für eine Konstante, gibt es hier keine befriedigende Möglichkeit, eine adäquate Übersetzung in Begriffsschrift zu finden. Man findet zwar in der Begriffsschrift das ähnliche Gesetz:⁹

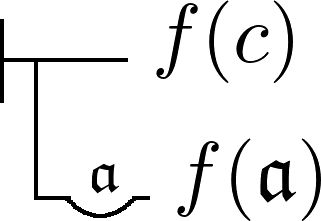
Diese Begriffsschriftformel soll aber Bedeutung haben, d.h. einen wahren Satz ausdrücken, wohingegen die modelltheoretische Formel nur syntaktisch ist. Die reine Syntax eines Axioms kann aber in der Begriffsschrift nicht ausgedrückt werden.

4  Allgemeinheit versus Formalität

Die erläuterten technischen Schwierigkeiten sind symptomatisch für einen grundlegenden Unterschied zwischen Freges Logikkonzeption und der modelltheoretischen Logik, der im Bereich der Philosophie der Logik verortet und mit dem Adjektivpaar allgemein/formal beschrieben werden kann.

Wenn Polimenov schreibt, dass der eigentliche Ausdruck der Allgemeinheit in den unbestimmt andeutenden Buchstaben liege,¹⁰ so weist er damit auf den wichtigen Punkt hin, dass Freges Begriffsschrift sich von der modernen Logik nicht nur durch das Notationssystem unterscheidet. Die Betitelung „Allgemeinheitsbuchstabe“ vermittelt jedoch den Eindruck, die andeutenden Buchstaben hätten die besondere Funktion, Allgemeinheit auszurücken. Nun gibt es aber in der Begriffsschrift neben den deutschen Buchstaben der Höhlung nur diese Allgemeinheit ausdrückenden, andeutenden Buchstaben. Es ist also nicht möglich, in der Begriffsschrift eine Formel allein aus logischem Vokabular aufzubauen, die nicht allgemein ist,¹¹ es sei denn die Allgemeinheit wird unter Zuhilfenahme eines Höhlungszeichens explizit verneint.¹² Diese Form der Allgemeinheit der Begriffsschriftformel spielt nämlich innerhalb von Freges Logikkonzeption eine ganz andere Rolle als die Allaussagen in der modernen Logik. So handelt zwar jede Begriffsschriftformel ebenso wie eine modelltheoretische Allaussage von dem gesamten Individuenbereich, da dieser „Individuenbereich“ in der Begriffsschrift aber alle referierenden Namen enthält, ist diese Allgemeinheit Ausdruck für die Allgemeingültigkeit. Somit sind jedoch allgemeine Sätze keine speziellen Begriffsschriftsätze, sondern alle rein logischen Begriffsschriftsätze¹³ sind allgemein qua Logik. Die allgemeingültigen Sätze der modelltheoretischen Logik sind die Axiome. Diese sind zwar qua Axiom in jedem beliebigen Individuenbereich wahr,¹⁴ aber an sich nur formal und nicht schon immer allgemein im dem Sinne, dass sie von irgendeiner Allheit handeln.

Um zu verstehen, warum Freges Begriffsschriftsätze umgekehrt allgemein, nicht aber formal sind, lohnt sich ein näherer Vergleich seines Standpunktes mit der Logik von Boole und Schröder. Hier äußert Frege explizit, er wolle keine „formale“ bzw. „abstrakte“ Logik schaffen, sondern mit seiner Logik Inhalte ausdrücken;¹⁵ und zwar nicht einfach indem Begriffe mit „schon vorhandenen Grenzlinien“ einfach kombiniert werden, sondern indem Begriffe erst durch Analyse der Bestandteile gebildet werden. Seine Allgemeinheitsdarstellung mit den andeutenden Buchstaben und den Höhlungszeichen war ihm dafür ein Instrumentarium von zentraler Bedeutung. Mithilfe seines Verständnisses von Allgemeinheit kann Frege Aussagen formalisieren, ohne Begriffe als extensional gegeben vorauszusetzen. Der Satz „Alle Menschen sind sterblich.“ ist nicht deswegen wahr, weil, wie Boole oder Schröder es deuten würden, die gegebene Menge der Menschen in der gegebenen Menge der Sterblichen enthalten ist, sondern weil von allen Gegenständen überhaupt diejenigen, die unter den Begriff Mensch fallen, auch immer unter den Begriff sterblich fallen. A=A gilt für Frege, weil für „A“ jeder Gegenstand überhaupt eingesetzt werden kann und nicht, weil die Identitätsrelation als die Menge aller 2-Tupel der Form (A,A) definiert ist, wobei A aus dem gegebenen, klar umgrenzten Individuenbereich stammt. So lässt sich Freges Kritik in „Booles rechnende Logik und meine Begriffsschrift“ verstehen, dass weder Leibniz noch Boole Inhalte hätten ausdrücken können, weil keiner von beiden seine Form der Allgemeinheitsdarstellung besäße¹⁶ und ihre Logik deswegen rein mechanisch sei.¹⁷ In dieser Kritik kommt eine Besonderheit der Frege’schen Logikverständnisses zum Ausdruck. Frege fordert mit seiner Logik objektiven Geltungsanspruch. Logik, so Frege, handle von der Wahrheit.¹⁸ Die Grundgesetze der Begriffsschrift sind also wahre Aussagen über alle Gegenstände. Deshalb kann es in Freges Logik auch keine rein formalen Gesetze geben. Die Gesetze ziehen schließlich ihren Geltungsanspruch aus der Wahrheit der in ihnen ausgedrückten Inhalte.¹⁹ In dieser Hinsicht unterscheiden sich logischen Sätze nicht von anderen Sätzen. Das Verhältnis von logischen Sätzen zu nicht logischen Sätze besteht bei Frege also nicht darin, dass die einen formal, die anderen inhaltlich sind, sondern darin, dass die einen den höchsten Grad von Allgemeinheit haben, die anderen weniger allgemein sind, da durch ein außerlogisches Prädikat, wie beispielsweise „Mensch“, der Individuenbereich eingeschränkt wird. Somit kann bei Frege nicht zwischen der Betrachtung der Wahrheit und der Gültigkeit unterschieden werden, wie es für die modelltheoretische Logik genuin ist.

Diese fehlende Unterscheidung verursacht die Probleme, die bei dem Versuch, Formeln aus beiden Logikkonzeptionen ineinander zu übersetzen, auftreten. Begriffsschriftgesetze sind weder, wie die Axiome in der modelltheoretischen Logik, rein formal, noch sind sie für irgendwelche Modelle gegebenen Individuenbereichen wahr. Somit liegt der eigentliche Grund für die Übersetzungsschwierigkeiten nicht in einer geringfügig unterschiedlichen Gebrauchsweise einzelner Zeichen, wie etwa des Quantors und des Höhlungszeichens, sondern in einer komplett unterschiedlichen Auffassung des Verhältnisses von Logik und Wahrheit.

5  Kann es „Quantoren“ in Freges Quantifikationstheorie geben?

Aus diesen Überlegungen lässt sich auch eine Antwort auf Polimenovs Titelfrage „Gibt es Quantoren in Freges Quantifikationstheorie?“ herleiten. Da für Frege die Logik von der Wahrheit handelt, kann es für ihn keine Trennung von Syntax und Semantik geben. Da es keine Trennung von Syntax und Semantik gibt, können Begriffsschriftsätze nicht in verschiedenen Modellen interpretiert werden, sondern sie handeln immer im weitesten Sinne von allem, also von allen Gegenständen überhaupt. Deswegen ist auch für die andeutenden Buchstaben schon immer eine Interpretation gegeben. Somit kann es keinen Operator geben, der ein Zeichen erst an einen Individuenbereich bindet. Also gibt es in Freges Begriffsschrift nicht nur keine Quantoren, sondern es kann auch keine Quantoren geben.²⁰

---